Duality in logic

If you've seen logic, you've seen the De Morgan laws:

¬(A ∧ B) ⇔ ¬ A ∨ ¬ B
¬(A ∨ B) ⇔ ¬ A ∧ ¬ B

and similarly for quantifiers. We often say that ∧ and ∨ are "De Morgan duals" to each other. In classical logic we also have

A ⇔ ¬ ¬ A

which is to say ¬ is an involution.

In this post, I want to emphasize a certain perspective on negation that gives a nice reading to De Morgan duality. This perspective shouldn't be too surprising, but making it explicit will be helpful for upcoming posts. What I'm going to do is split the judgment ⊢ A, which represents an assertion that A is true, into two judgments:





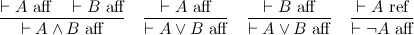
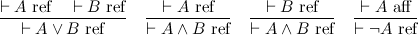
The two judgments are affirmation and refutation, respectively. Thus we've put truth and falsehood on common footing, and in particular, we can construct a direct refutation of a proposition. For instance, to refute A ∧ B is to refute either of A or B.

These two judgments capture the essence of both De Morgan duality, and the involutive nature of negation. The point is that conjunction and disjunction are two sides of the same coin, the difference being whether you are affirming or refuting a proposition. Negation switches between the two modes of proof, and because there are only two modes, it is an involution.

In general, we can distinguish between positive and negative polarities, so that affirmation is positive and refutation negative. Polarities show up all over the place. A common example is game semantics, where the validity of a proposition is modeled by the player (trying to affirm it) has a winning strategy against the opponent (trying to refute it). Polarity, it turns out, is also very important in understanding linear logic; stay tuned.