As a first step toward sequent calculus, we alter notation, writing ⊢ A for ⊢ A aff and A ⊢ for ⊢ A ref. We then generalize in two ways. First, rather than a single formula A, we will allow a multiset of formulas Γ. The choice of multisets, rather than sets, is to allow for an analysis of structural rules later. The reading of ⊢ Γ is "some formula in Γ is affirmable" and similarly for Γ ⊢. This generalization is motivated by the need to internalize compound formulas into smaller pieces: there should be some relationship between ⊢ A ∨ B and ⊢ A, B (thanks, Neel, for that insight). Though, as we will see, this relationship is more subtle than it appears at first.
Once we allow multiple formulas on one side of the turnstile, though, we are forced to allow formulas on both sides. The culprit is the rule for negation -- even if we force its premise to stay on one side, its conclusion refuses to:
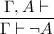
But now, our two judgments have become one! Instead of playing either as affirmer or refuter, we play as both at once. We will deduce sequents Γ ⊢ Δ, with the meaning that either some A ∈ Γ is refutable or some A ∈ Δ affirmable. The empty sequent ⊢ is, perforce, unprovable. The following rules, which determine the meaning of our three primary connectives, generalize our earlier rules to sequents:
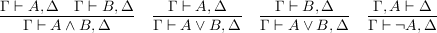
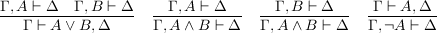
To bring the calculus to life, we need axioms -- and in fact, a single one will suffice:
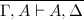
This rule has the somewhat startling reading "either A is refutable or it is affirmable," which makes it sound as if we have baked in classical principles from the start. But there is a somewhat Tarskian phenomenon here: our reading of the rule used the word "or" in a metalogical way, which has quite different force from the sequent ⊢ A ∨ ¬A. As it turns out, the axiom we have given occurs in both classic and intuitionistic sequent calculus.
With that, we have a complete kernel of sequent calculus. There is much more to say, of course. For instance, this calculus is classical, and making it intuitionistic is a matter of breaking the symmetry between affirmation and refutation, moving to sequents Γ ⊢ A. This situation stands in strong contrast to natural deduction, where the difference comes down to the inclusion of an axiom, rather than structural properties.
Girard discovered linear logic in part through an analysis what, precisely, must be restricted to get intuitionistic sequent calculus. His famous decomposition of intuitionistic implication, A → B = (!A) ⊸ B, tells us that the heart of the matter is restricting the structural rules (weakening and contraction, which we have baked in) for affirmation, but not for refutation. But there is an even deeper story, based on polarity, which will allow us to view classical logic through a constructive lens...
